Hawaiian earring
In mathematics, the Hawaiian earring H is the topological space defined by the union of circles in the Euclidean plane R2 with center (1/n, 0) and radius 1/n for n = 1, 2, 3, .... The space H is homeomorphic to the one-point compactification of the union of a countably infinite family of open intervals.
The Hawaiian earring can be given a complete metric and it is compact. It is path connected but not semilocally simply connected.
The Hawaiian earring looks very similar to the wedge sum of countably infinitely many circles; that is, the rose with infinitely many petals, but those two spaces are not homeomorphic. The difference between their topologies is seen in the fact that, in the Hawaiian earring, every open neighborhood of the point of intersection of the circles contains all but finitely many of the circles. It is also seen in the fact that the wedge sum is not compact: the complement of the distinguished point is a union of open intervals; to those add a small open neighborhood of the distinguished point to get an open cover with no finite subcover.
Fundamental group
The Hawaiian earring is not simply connected, since the loop parametrising any circle is not homotopic to a trivial loop. Thus, it has a nontrivial fundamental group G.
The Hawaiian earring H has the free group of countably infinitely many generators as a proper subgroup of its fundamental group. G contains additional elements which arise from loops whose image is not contained in finitely many of the Hawaiian's earrings circles; in fact, some of them are surjective. For example, the path that on the interval [2−n, 2−(n−1)] circumnavigates the nth circle.
It has been shown that G embeds into the inverse limit of the free groups with n generators, Fn, where the bonding map from Fn to Fn−1 simply kills the last generator of Fn. However G is not the complete inverse limit but rather the subgroup in which each generator appears only finitely many times. An example of an element of the inverse limit which is not an element of G is an infinite commutator.
G is uncountable, and it is not a free group. While its abelianisation has no known simple description, G has a normal subgroup N such that 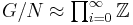 , the direct product of infinitely many copies of the infinite cyclic group (the Baer–Specker group). This is called the infinite abelianization or strong abelianization of the Hawaiian earring, since the subgroup N is generated by elements where each coordinate (thinking of the Hawaiian earring as a subgroup of the inverse limit) is a product of commutators. In a sense, N can be thought of as the closure of the commutator subgroup.
, the direct product of infinitely many copies of the infinite cyclic group (the Baer–Specker group). This is called the infinite abelianization or strong abelianization of the Hawaiian earring, since the subgroup N is generated by elements where each coordinate (thinking of the Hawaiian earring as a subgroup of the inverse limit) is a product of commutators. In a sense, N can be thought of as the closure of the commutator subgroup.
References
- Cannon, J. W.; Conner, G. R. (2000), "The big fundamental group, big Hawaiian earrings, and the big free groups", Topology and its Applications 106 (3): 273–291, doi:10.1016/S0166-8641(99)00104-2.
- Conner, G.; Spencer, K. (2005), "Anomalous behavior of the Hawaiian earring group", Journal of Group Theory 8 (2): 223–227, doi:10.1515/jgth.2005.8.2.223.
- Eda, K. (2002), "The fundamental groups of one-dimensional wild spaces and the Hawaiian earring", Proceedings of the American Mathematical Society 130 (5): 1515–1522, doi:10.1090/S0002-9939-01-06431-0.
- Eda, K.; Kawamura, K. (2000), "The singular homology of the Hawaiian earring", Journal of the London Mathematical Society (Ser. 2) 62 (1): 305–310, doi:10.1112/S0024610700001071.
- Fabel, P. (2005), "The topological Hawaiian earring group does not embed in the inverse limit of free groups", Algebraic & Geometric Topology 5: 1585–1587, doi:10.2140/agt.2005.5.1585.
- Morgan, J. W.; Morrison, I. (1986), "A van Kampen theorem for weak joins", Proceedings of the London Mathematical Society (Ser. 3) 53 (3): 562–576, doi:10.1112/plms/s3-53.3.562.
- Biss, Daniel K. (2000), "A generalized approach to the fundamental group", American Mathematical Monthly (Mathematical Association of America) 107 (8): 711–720, doi:10.2307/2695468, JSTOR 2695468.